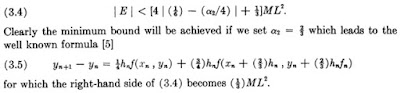Earlier this semester, I was teaching second-order Runge-Kutta methods, when one of my students, Eitan Lees, noticed that the formulas I wrote down for
Ralston's method, was inconsistent with the formula on
wikipedia and
elsewhere on the web. This form can be written in the famous "RK Tableau" form as: \[\begin{array}{c|cc}
0 & 0 & 0 \\
2/3 & 2/3 & 0 \\
\hline
& 1/4 & 3/4 \\
\end{array}.\] However, there are
other sources on the web, and the famous textbook of
Chapra and Canale, which give a different formula (and the one I happened to use in my class, probably because I picked it up from that very source). This has the form: \[\begin{array}{c|cc}
0 & 0 & 0 \\3/4 & 3/4 & 0 \\
\hline
& 1/3 & 2/3 \\
\end{array}.\] Ralston's method is special, because
it promises to be the "best" explicit RK2 method. What is more, I distinctly remember seeing an example in the C&C textbook pitting their version of the method against the competition (other explicit RK2 methods) and showing that it was indeed the best!
So which of the two forms is correct. There can't really be two best RK2 methods, can there?
I looked at the original source,
the 1962 paper by Ralston, and the book "
A First Course in Numerical Analysis" by Ralston, and found that the original versions favor the wikipedia form.
 |
| From Ralston, 1962; more on this later. |
Surprisingly, Chapra and Canale cite these two sources before they put down their (what turns out to be incorrect) form.
Background on Explicit RK2
To back up a little bit, the family of second order RK methods are given by,\[y_n = y_{n-1} + h (a_1 k_1 + a_2 k_2),\] where, \[\begin{eqnarray}
k_1 & = & f(t_{n-1}, y_{n-1}) \\
k_2 & = & f(t_{n-1} + p_2 h , y_{n-1} + q_{21} k_1 h)
\end{eqnarray}.\] Using Taylor series expansion, and linearizing \(k_2\) it can be shown that coefficients have to satisfy the constraints, \[\begin{align*}
a_1 + a_2 & = 1 \\
a_2 p_2 & = \frac{1}{2} \\
a_2 q_{21} & = \frac{1}{2}
\end{align*}.\] If one of the four unknowns is specified (say \(a_2\)) the other unknowns can be determined easily.
So there is a family of RK2 methods.
- Heun's Method: \[a_2 = 1/2; \implies a_1 = 1/2,~ p_2 = q_{21} = 1.\]
- Midpoint Method: \[a_2 = 1; \implies a_1 = 0, p_2 = q_{21} = 1/2.\]
- Ralston's Method (1 - 1962 paper): \[a_2 = 3/4; \implies a_1 = 1/4, p_2 = q_{21} = 2/3.\]
- Ralston's Method (2 - C&C text): \[a_2 = 2/3; \implies a_1 = 1/3, p_2 = q_{21} = 3/4.\]
Error Analysis
One can follow Ralston's analysis in his 1962 paper. In the paper he shows that his method can be obtained by trying to minimize a bounding function
\[|E| < \left(4 \left| \frac{1}{6} - \dfrac{p_2}{4} \right| + \dfrac{1}{3} \right)ML^2,\] I have rewritten this portion (which can be seen from the picture excerpted from the original paper above) in my notation. Note that \(p_2\) in our case is the same as \(\alpha_2\) in the 1962 paper.
It is easy to see that the minimum is obtained at \(p_2 = 2/3\). In fact, one can plot this error bound function, and locate the different RK2 methods on it.
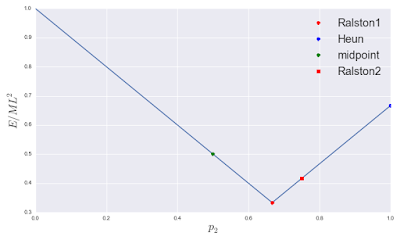
One can see the location of the actual optimum (2/3), the Ralston's method reported in Chapra and Canale (red square = Ralston2), and the other two RK2 methods.
In terms of error bound, one notes that ordering the method from most to least accurate, we have:
- Ralston 1 (1962 form)
- Ralston 2 (C&C text)
- Midpoint Method
- Heun's Method
Test Example
Chapra and Canale do a numerical example in which their version of Ralston's method (Ralston2) outperformed both Heun's and midpoint method. \[y'(t) = -2 t^3 + 12 t^2 - 20t + 8.5,~~~y(0) = 1.\] This is an interesting example because the RHS is only a function of \(t\), and this is in fact a quadrature problem masquerading as an initial value problem.
It is simple enough that one can easily find the exact analytical solution, and hence compute the true error in a numerical method. All RK2 methods are second order accurate (\(\mathcal{O}(h^2)\)), where h is the step-size.
Here is how the 4 different RK2 methods perform:
As you see, the order of accuracy of Heun's method, midpoint method, and the C&C version of Ralston method is as expected from the error analysis. The dashed line has a slope of 2, and shows that the three methods are second ordered.
The true Ralston method (Ralston1) is an outlier and is far more accurate than the other three. Curiously, it also has a higher slope. The slope of the dotted line is 3. What happened was that the choice of \(p_2\) reduced the constant in front of the \(\mathcal{O}(h^2)\) term to such an extent that it neutralized that term, and conspired to give us an serendipitous boost of one order in accuracy. The dotted line has a slope of 3.
Conclusion
A possible origin of this discrepancy is that Ralston called \(p_2\) as \(\alpha_2\) in his original paper. It is possible that the \(\alpha_2 = 2/3\) got confused with \(a_2 = 2/3\) in the C&C textbook. Given the popularity of the textbook, the mistake proliferated inadvertently.
This is why you need smart students constantly questioning received wisdom.